周赛笔记11/13/2022

6234.最小公倍数为 K 的子数组数目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。

子数组 是数组中一个连续非空的元素序列。数组的最小公倍数 是可被所有数组元素整除的最小正整数。

示例 1 ：

输入：nums = [3,6,2,7,1], k = 6
输出：4
解释：以 6 为最小公倍数的子数组是：
- [3,6]
- [3,6,2]
- [6,2]
- [6]

//两个for循环扫描
class Solution {
    public int subarrayLCM(int[] nums, int k) {
        int ans =0;
        int n=nums.length;
        for(int i=0;i<n;i++){
            if(nums[i]==k) ans++;
            int temp=nums[i];
            for(int j=i+1;j<n;j++){
                //最小公倍数的传递性，a,b,c的最小公倍数为：a,b的最小公倍数k与c的最小公倍数
                temp=minMul(temp,nums[j]);
                if(temp==k) ans++;
            }
        }
        return ans;
    }
    //可以记住这个算法
    //利用最大公约数求最小公倍数
    int minMul(int a, int b){
        int sum = a*b;
        return sum/gcd(a,b);
    }
    //辗转相除法求最大公约数
    int gcd(int a,int b){
        return (b==0)?a:gcd(b,a%b);
    }
}

6235.逐层排序二叉树所需的最少操作数目

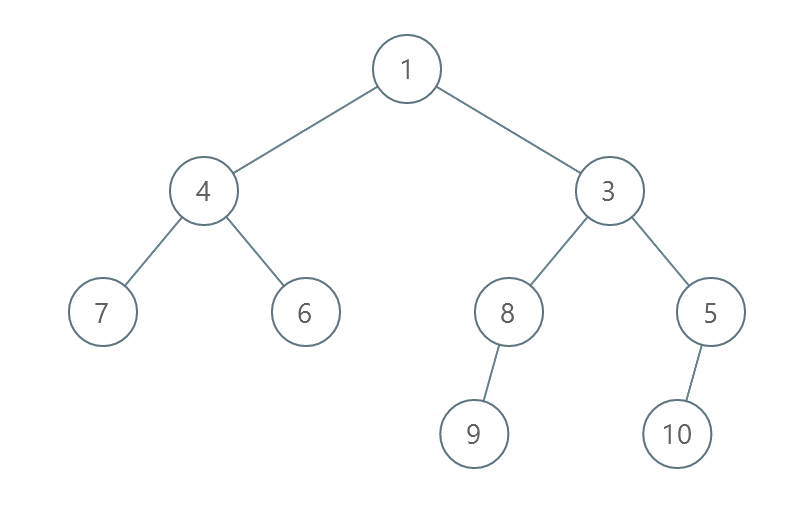
给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

//复习二叉树的层序遍历
class Solution {
    //层序遍历，生成每层的数组记录，对数组记录进行操作，记录操作次数
    public int minimumOperations(TreeNode root) {
        if(root==null) return 0;
        int res = 0;
        Deque<TreeNode> q = new ArrayDeque<>();
        q.add(root);
        while(q.peek()!=null){
            int n = q.size();
            int[] record = new int[n];
            for(int i=0;n>0;n--){
                TreeNode node = q.poll();
                record[i++] = node.val;
                if(node.left != null) q.add(node.left);
                if(node.right !=null)q.add(node.right);
            }
            res+=count(record);
        }
    return res;
    }
    //记录将数组变为有序的最小交换次数
    int count(int[] record){
        //比较与排序过的数组的索引差异，不断交换，直到相同
        HashMap<Integer,Integer> map = new HashMap();
        int[] sorted = record.clone();
        Arrays.sort(sorted);
        int count=0;
        for(int i=0;i<record.length;i++) map.put(sorted[i],i);
        for(int i=0;i<record.length;i++){
            while(true){
                int index = map.get(record[i]);
                if(index!=i){
                    count++;
                    swap(record,index,i);
                }
                else break;
            }
        }
        return count;
    }
    void swap(int[] nums, int i,int j){
        int temp = nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }
}